どもはじめまして、タローです。
flashとの出会いから早1年、flash好きが昂じてそのまま入社して2月目に入ろうとしている、2009新卒の新入社員です。

先輩のやっているコンテンツで計算のお手伝いをしたことがあったので、今回は座標変換のお話について少ししようと思います。四角形と四角形がぴったり重なりあいたいという気持ちをどう説明するか、ということで「アフィン変換」と「射影変換」のお話をします。図やサンプルもつけてみましたので是非ご覧下さい。

アフィン変換って？

詳しくは、livedocsのMatrixのところにある図のような変換が出来て、任意の平行四辺形から任意の平行四辺形への変換が可能です。つまり、平行な直線が平行な直線に移るような変換です。

このlivedocsのページですが、ここにある図は間違っていて、skewの所の説明ですが、 下の図のようなものが正しいものとなります。

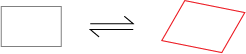
射影変換

アフィン変換では歪んだ四角形を平行四辺形や長方形に写すことはできません。歪んだ僕から真っ直ぐな君に・・・

つまり、射影変換は必ずしも2つの直線の平行関係を保たない変換です。ここでサンプルを見てみましょう。

赤い四辺形と青の四辺形を互いに対応させています。赤い四辺形の中にマウスを持ってくると、青い四辺形の中に対応する緑の点が写り込みます。頂点と頂点が対応するように作ってあります。台形補正というのは、台形から長方形に対応させるイメージになります。

少しだけ専門的な話をすると、アフィン変換というのは線形な変換で、

で写される点(x,y)から(x', y')への変換です。一方射影変換は、

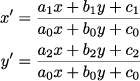
とう形の変換なので、実はアフィン変換というのは射影変換の特殊な形です。(の場合)この変換の9つの係数a0～c2が決まれば射影変換が決まります。そこで上のサンプルでは、赤の4点から青の4点に写るという関係で式を立てて射影変換をするということをしています。1点にはx座標とy座標がそれぞれあるので、これらは8つの式となります。9つの未知数に8つの式ですから、変数が一つ残ってしまうのですが、射影変換の式は分数なので、約分してしまえば、変数は消えるので変換は一次有理関数の同値類として一つに定まります。では、最後にもう一つ別のサンプルを見て射影変換のイメージをつかんでみましょう。

ということで、射影変換とアフィン変換のイメージが湧きましたでしょうか？ちょっと説明不足なところもありますが、第1回目の投稿はここら辺で終わりにします。サンプルに登場するAIR本もよろしくお願いします。