どうも。こんにちは。梅雨明けも宣言されたそうで、いよいよ暑くなりますね。今回は単振動方程式方程式を用いた最適化のお話です。 高校物理でも登場するバネの方程式、単振動方程式 を簡単な四則計算に分解する方法を紹介します。

まず色々な数学的背景を押しやって、イメージだけ説明すると、物体の位置x、速度v、加速度aの関係は

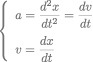
となるので、asの式で考えると、

v += a;
x += v;

という風になります。ここで単振動の微分方程式から、

a = -K * x;

であるから、あわせると、

v -= K * x;
x += v;

という風になります。下がサンプルで、初期値(_v, _y)やKなんかを変えて挙動が変わることが分かります。

ここでのポイントはvに対して最初の式で破壊的な操作を行っていることです。

v_temp = v;
v -= K * x;
x += v_temp;

等とすると、ずれてしまいます。これは、この計算をn回した後のx, vをそれぞれ、x_n, v_nとすると、

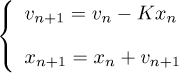
この漸化式の固有値は、

であり、先ほどの数列の一般解は

となります。ここでこれらの固有値の絶対値がそれぞれ1であることがポイントで、

これにより、これら二つの固有値は、

とあらわすことが出来るので、x_nは、

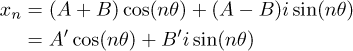
となります。ここで思い出して欲しいのが、単振動の方程式の一般解とこの漸化式の解が類似していることです。実はこの二つの解空間というのは同型であり、この方法というのは近似計算等ではなく、単振動方程式の離散的な解ということになります。だから、値が非常に正確であり、かつ高速なのです。一方vに対して破壊的操作を行わなかった場合は、

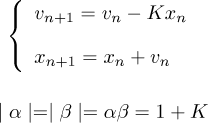
のように絶対値が1+Kとなってしまい、計算の度にずれてしまいます。直感的に速度、加速度と捕らえて上手くやろうとしても、ある程度下のレイヤーの知識が無いと誤差の修正で引っかかってしまうことになりますが、sinやcosにはこういう計算使ってみるのも一手ではないでしょうか。色々応用があって円運動なんかもこの手の単純化ができます。むつかしい話が続いたので最後に一つこの計算を利用してcheckmateやってみました。Möbiusの輪を描きました。